Answer:
0.3991
Explanation:
Given that the weights of the fish in a certain lake are normally distributed with a mean of 18 lb and a standard deviation of 18 .
we know that when a sample is taken mean would be the same but std error would vary
when a sample of size 15 is taken we have

Standard error of sample =
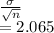
the probability that the mean weight will be between 16.6 and 21.6 lb

So we get the required probability as
0.3991