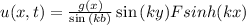Question

Find the solution u(x, y) of Laplace's equation in the rectangle 0 < x < a, 0 < y < b, that satisfies the boundary conditionsu(0, y) = 0, u(a, y) = 0, 0< y< b,u(x, 0) = 0, u(x, b) = g(x), 0 ≤ x ≤ a.

Answer 1

`u(x,t) = (g(x))/(sin((kb)))sin((ky)) Fsinh{(kx)}`

Explanation:

The Laplace's equation in rectangular coordinates is:

`(\partial^2 u)/(\partial x^2) +(\partial^2 u)/(\partial y^2) = 0`

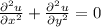
For the solution, we assume that u can be write as

`u(x,y) = X(x)Y(y)`

Replace

`Y(y)(d^2X)/(dx^2) +X(x)(d^2Y)/(dy^2) =0`

Divide
`X(x) Y(y)`

`(1)/(X(x))(d^2X)/(dx^2)= -(1)/(Y(y))(d^2Y)/(dy^2)`

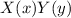
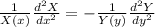
The only way that this can be true, is that every term is the same constant, so we say that

`(1)/(X(x))(d^2X)/(dx^2) =  -(1)/(Y(y))(d^2Y)/(dy^2) = k^2`

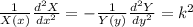
With
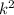`k^2` a constant.

Now, we solve every part. For
`X(x)`

`(d^2X)/(dx^2) = k^2X(x)`

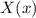
The solution is:

`X(x) = Ee^(kx) + De^(-kx)`

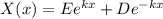
For
`Y(y)`

`(d^2Y)/(dy^2) = -k^2Y(y)`

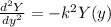
Is the differential equation for a harmonic oscillator, so the solution is

`Y(y) = Acos(ky) + Bsin(ky)`

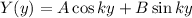
Now, we evaluate the boundary conditions:

`u(x,0) = 0 \rightarrow Y(0) = 0`

`Y(0) = Acos(0) + Bsin(0) = 0; A = 0`

`Y(y) = Bsin(ky)`

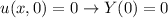
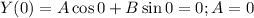
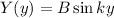
The other

`u(x,b) = 0 \rightarrow Y(b) = 0`

`Y(b) = B\sin({kb}) = g(x); B = \frac{g(x)}{sin({kb})}`

`Y(y) = \frac{g(x)}{\sin({kb})} sin{(ky)}`

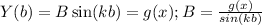
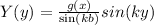
For
`X(x)`:

`u(0,y) = 0 \rightarrow X(0) =0`

`X(0) = Ee^(0) + De^(-0) =0; E+D=0`

`E = -D`

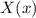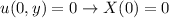
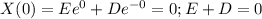
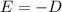
So,
`X(x) = E(e^(kx) - e^(-kx) ) = 2Esinh(kx) = Fsinh(kx))`

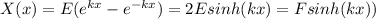
The other condition:

`u(a,y) = 0 \rightarrow X(a) = 0`

`X(a) = F(sinh{(ka)}) = 0`

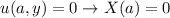
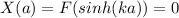
So,

`u(x,t) = (g(x))/(sin((kb)))sin((ky)) Fsinh{(kx)}`