Question

Solve the equation by graphing. If exact roots cannot be found, state the consecutive integers between which the roots are located. 2x^2-3x+4=0

Answer 1

There are NO real roots for this equation. The only roots have imaginary parts and therefore cannot be represented on the real x-axis.

Explanation:

We notice that the expression on the left of the equation is a quadratic with leading term
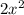`2x^2`, which means that its graph is that of a parabola with branches going up.

Therefore, there can be three different situations:

1) if its vertex is ON the x axis, there would be one unique real solution (root) to the equation.

2) if its vertex is below the x-axis, the parabola's branches are forced to cross it at two locations, giving then two real solutions (roots) to the equation.

3) if its vertex is above the x-axis, it will have NO real solutions (roots) but only non-real ones.

So we proceed to examine the vertex's location, which is also a great way to decide on which set of points to use in order to plot its graph efficiently.

We recall that the x-position of the vertex for a quadratic function of the form
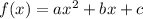`f(x)=ax^2+bx+c` is given by the expression:

`x_v=(-b)/(2a)`

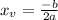
Since in our case
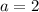`a=2` and
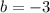`b=-3`, we get that the x-position of the vertex is:

`x_v=(-b)/(2a)\\x_v=(-(-3))/(2(2))\\x_v=(3)/(4)`

Now we can find the y-value of the vertex by evaluating this quadratic expression for x = 3/4:

`y_v=f((3)/(4))=2( (3)/(4))^2-3((3)/(4))+4\\f((3)/(4))=2( (9)/(16))-(9)/(4)+4\\f((3)/(4))=(9)/(8)-(9)/(4)+4\\f((3)/(4))=(9)/(8)-(18)/(8)+(32)/(8)\\f((3)/(4))=(23)/(8)`

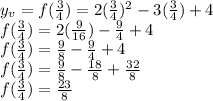
This is a positive value for y, therefore we are in the situation where there is NO x-axis crossing of the parabola's graph, and therefore no real roots.

We can though estimate a few more points of the parabola's graph in order to complete the graph as requested in the problem. For such we select a couple of x-values to the right of the vertex, and a couple to the right so we can draw the branches. For example: x = 1, and x = 2 to the right; and x = 0 and x = -1 to the left of the vertex:

`f(-1) = 2(-1)^2-3(-1)+4= 2+3+4=9\\f(0)=2(0)^2-3(0)+4=0+0+4=4\\f(1)=2(1)^2-3(-1)+4=2-3+4=3\\f(2)=2(2)^2-3(2)+4=8-6+4=6`

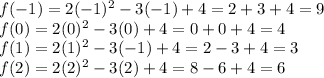
See the graph produced in the attached image.