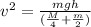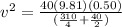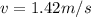Answer:
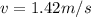
Step-by-step explanation:
While mass is falling downwards there is no frictional loss so here we can use mechanical energy conservation
So change in gravitational potential energy = gain in kinetic energy of the system
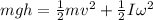
for uniform cylinder we will have
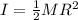
now we have
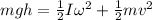
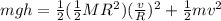
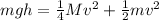
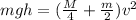
now we have