Question

A jewel necklace contains only emeralds, rubies, and diamonds. If the ratio of emeralds to diamonds is 2:7 and the ratio of diamonds to rubies is 3:2, then which of the following could not be the number of jewels on the necklace?(A) 41(B) 81(C) 82(D) 123(E) 205

Answer 1

B) 81

Explanation:

If you have a jewelry necklace with only emeralds, rubies and diamonds (N = R + E + D), If the ratio of emeralds to diamonds is 2: 7 (7E = 2D) and the ratio of diamonds to rubies is 3: 2 (3R = 2D), then which of the following could not be the number of jewels on the necklace? (A) 41 (B) 81 (C) 82 (D) 123 (E) 205

Knowing that:

N=R+E+D; 2D=7E: 2D=3R and 7E=3R Then:

`N=(2)/(3) D+(2)/(7)D+D=(14D+6D+21D)/(21)  =(41)/(21)D\\N= R+(3)/(7)R+(3)/(2)R=(14R+6R+21R)/(14)  =(41)/(14)R\\ N=(7)/(3)E+E+(7)/(2)E=(14E+6E+21E)/(6)  =(41)/(6)E`

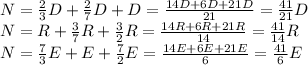
if we begin to substitute the values ​​given in the equation: N = R + E + D, we will observe that for all the values ​​it is fulfilled (whole numbers), but it is only for N = 81 where these values ​​are fractionated

:

FOR N=81

D=(21*81)/41 ≅ 41.487....

R=(14*81)/41 ≅ 27.658...

E=( 6*81)/41 ≅ 1 1.853....

Note: we are told that it ONLY contains rubies, emeralds and diamonds