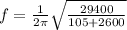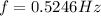To develop this problem it is necessary to apply the concepts related to frequency from Hooke's law.
By Hooke's law we know that the Force is defined as
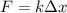
Where,
k = Spring constant
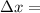 Displacement
Displacement
at the same time Force can be defined by Newton's second law as,
F = mg
Where,
m = mass
g = gravity
Equating we have
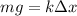
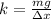
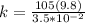
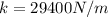
Frequency and oscillation can be defined as
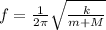
Then replacing,