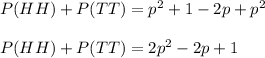Answer:
-First player wins:
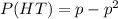
-Neither player wins:
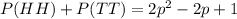
Explanation:
Applying the 4 step method:
Step 1: Identify events for which probability is to be determined:
- First player wins: First coin is heads, second coin is tails (HT)
- Neither player wins: Both coins are heads or both coins are tails (HH or TT)
Step 2: Calculate total number of possible outcomes:
Four possible outcomes: HH, HT, TT, TH
Step 3: Calculate probability of each event
Since the probability of a coin coming up heads is 'p':
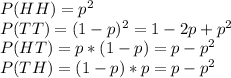
Step 4: Add probability of each event
-First player wins:
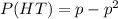
-Neither player wins: