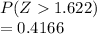Question

Suppose we have a factory that produces lightbulbs and that each bulb independently has a 5% probability of dying after 4 years. Suppose that during a particular year we produce 1250 bulbs. Let X be the RV for the number of bulbs still working after 4 years. Use the CLT to approximate P(X > 1200).

Answer 1

0.4166

Explanation:

Given that we have a factory that produces light bulbs and that each bulb independently has a 5% probability of dying after 4 years.

i.e. prob = 0.05 for each bulb for dying since independent is given

Also there are only two outcomes either working or dying.

X no of bulbs still working is binomial with

constant probability p = 0.95, q = 0.05 and n = 1250

np =
`1250(0.95) = 1187.5`

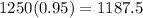
nq = 62.5

Both are >5. Hence X can be approximated to normal with

mean = 1187.5 and variance =npq = 59.375

std dev = 7.7055

Using central limit theorem we find that X is N(1187.8, 7.7055)

P(X > 1200)

=
`P(Z>1.622)\\=0.4166`