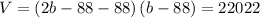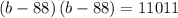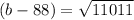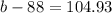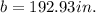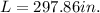Question

A rectangular piece of sheet metal has a length that is 88 in. less than twice the width. A square piece 44 in. on a side is cut from each corner. The sides are then turned up to form an uncovered box of volume 968968 in. cubed. Find the length and width of the original piece of metal.

Answer 1

Explanation:

Let L and b be the Length and breadth of Rectangular Piece of sheet metal

also
`L=2b-88`

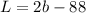
Square piece of 44 in. is cut from each corner

thus New length of cuboid is
`L'=L-2* 44`

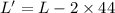
Breadth of Cuboid
`b=b-2* 44`

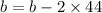
Height of breadth is
`h=44 in.`

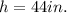
Volume of Cuboid
`V=968968`

`V=\left ( L-2\cdot 44\right )\cdot \left ( b-2\cdot 44\right )\cdot \left ( 44\right )=968968`

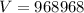
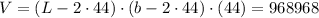
substitute the value of L i n volume

`V=\left ( 2b-88-88\right )\left ( b-88\right )=22022`

`\left ( b-88\right )\left ( b-88\right )=11011`

`\left ( b-88\right )^2=11011`

`\left ( b-88\right )=√(11011)`

`b-88=104.93`

`b=192.93 in.`

`L=297.86 in.`