Question

A simple pendulum consists of a point mass, m, attached to the end of a massless string of length L. It is pulled out of its straight-down equilibrium position by a small angle theta and released so that it oscillates about the equilibrium position in simple harmonic motion with frequency f. What will happen to the frequency if the same pendulum oscillates in simple harmonic motion on the moon instead of on Earth?

Answer 1

here on the surface of moon the gravity decreases so the frequency of oscillation will also decrease

Step-by-step explanation:

As we know that frequency of oscillation of the simple pendulum is given as

`f = (1)/(2\pi)\sqrt{(g)/(L)}`

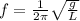
here we know

g = acceleration due to gravity at the surface of the planet

L = length of the pendulum

Now we know that the pendulum is on the surface of earth then gravity is given as

`g = 9.81 m/s^2`

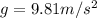
now when same pendulum is taken to the surface of the moon then we have

`g_(moon) = (g)/(6)`

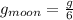
so here on the surface of moon the gravity decreases so the frequency of oscillation will also decrease