Question

William Tell shoots an apple from his son's head. The speed of the 105-g arrow just before it strikes the apple is 24.3 m/s, and at the time of impact it is traveling horizontally. If the arrow sticks in the apple and the arrow/apple combination strikes the ground 9.50 m behind the son's feet, how massive was the apple? Assume the son is 1.85 m tall.

Answer 1

To develop this problem it is necessary to apply the concepts related to conservation of the Moment and the cinematic equations of movement description. By definition we know that the conservation of the moment is given by

`m_1V_1 = (m_1+m_2)V`

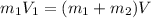
Where,

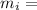`m_i =` Mass

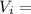`V_i =` Velocity

From the kinematic equations of motion we know that displacement as a function of acceleration (in this case gravity) is given by,

`h = (1)/(2) gt^2`

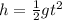
Where h is the height, g the gravity and t the time,

`t= \sqrt{(2h)/(g)}`

The horizontal velocity would be given as,

`V = (X)/(t)`

`V = \frac{X}{\sqrt{(2h)/(g)}}`

`V = \frac{9.5}{\sqrt{(2(1.85))/(9.8)}}`

`V= 5.83m/s`

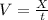
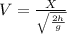
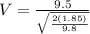
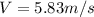
Replacing in our first equation we have that

`m_1V_1 = (m_1+m_2)V`

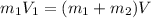
Solving for
`m_2`

`m_2 = m_1((V1)/(V) - 1)= 0.105 ((24.3)/(5.83) - 1)`

`m_2=0.332kg = 332g`

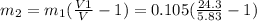
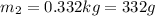
Therefore the apple had 332g.