Question

Two points along a straight stick of length 36 cm are randomly selected. The stick is then broken at those two points. Find the probability that all of the resulting pieces have length at least 6.5 cm.

Answer 1

0.2103

Explanation:

Since the Distribution is uniform (as it is along a straight line), so we can consider the probabilities as direct areas.

It can represented by a square having an area of
`36^(2)`.

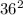Area of whole stick = Length x Breadth = 36 x 36 =1296
`cm^(2)`

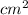
This area is equal to probability of 1.

Now when two points are randomly selected, they can be represented as :

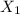`X_(1)` and
`X_(2)`

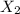
After breaking from two points, there will be three pieces of stick

1 piece Least length = 6.5 cm

3 piece length = 6.5 x 3 = 19.5 cm

Area of pieces with at least 6.5cm length =
`(Length .of. whole .stick- length .of. 3. pieces)^(2)` =
`(36 - 19.5)^(2)` =
`(16.5 cm)^(2)` =
`272.25 cm^(2)`

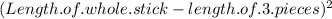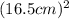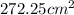
Probability of resulting pieces having at least 6.5 length = P (6.5 length) =
`((Area -of -pieces -with-6.5 -length))/(Area-of-stick)`

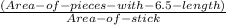
P (6.5 length) =
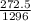`(272.5)/(1296)` = 0.2103

which is the probability that all of the resulting pieces have length at least 6.5 cm.