Question

Three-point charges have equal magnitudes, two being positive and one negative. These charges are fixed to the corners of an equilateral triangle, as the drawing shows. The magnitude of each of the charges is 5.1 µC, and the lengths of the sides of the triangle are 2.2 cm. Calculate the magnitude of the net force that each charge experiences.

Answer 1

Step-by-step explanation:

q1 = - 5.1 micro coulomb

q2 = 5.1 micro coulomb

q3 = 5.1 micro coulomb

d = 2.2 cm

Let these charges are placed at A, B and C of the vertices of an equilaterla triangle

Force on A:

`F_(AB)=(kq_(1)q_(2))/(d^(2))`

`F_(AB)=\frac{9* 10^(9)* 5.1* 10^(-6)* 5.1* 10^(-6)}}{0.022^(2)}`

`F_(AB) = 483.65`

`F_(AC)=(kq_(1)q_(3))/(d^(2))`

`F_(AC)=\frac{9* 10^(9)* 5.1* 10^(-6)* 5.1* 10^(-6)}}{0.022^(2)}`

`F_(AC) = 483.65`

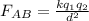
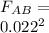
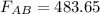
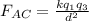
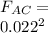
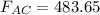
The net force acting on q1 is given by

`F_(1)=\sqrt{F_(AB)^(2)+F_(AC)^(2)+2F_(AB)F_(AC)Cos60}`

`F_(1)=\sqrt{483.65^(2)+483.65^(2)+2* 483.65* 483.65* 0.5}`

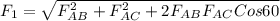
F1 = 837.71 N

Force on B:

`F_(BA)=(kq_(1)q_(2))/(d^(2))`

`F_(BA)=\frac{9* 10^(9)* 5.1* 10^(-6)* 5.1* 10^(-6)}}{0.022^(2)}`

`F_(BA) = 483.65`

`F_(BC)=(kq_(1)q_(3))/(d^(2))`

`F_(BC)=\frac{9* 10^(9)* 5.1* 10^(-6)* 5.1* 10^(-6)}}{0.022^(2)}`

`F_(BC) = 483.65`

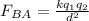
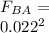
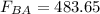
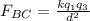
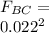
The net force acting on q1 is given by

`F_(2)=\sqrt{F_(BA)^(2)+F_(BC)^(2)+2F_(BA)F_(BC)Cos120}`

`F_(2)=\sqrt{483.65^(2)+483.65^(2)-2* 483.65* 483.65* 0.5}`

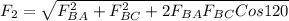
F2 = 483.65 N

Force on C:

`F_(CB)=(kq_(1)q_(2))/(d^(2))`

`F_(CB)=\frac{9* 10^(9)* 5.1* 10^(-6)* 5.1* 10^(-6)}}{0.022^(2)}`

`F_(CB) = 483.65`

`F_(CA)=(kq_(1)q_(3))/(d^(2))`

`F_(CA)=\frac{9* 10^(9)* 5.1* 10^(-6)* 5.1* 10^(-6)}}{0.022^(2)}`

`F_(CA) = 483.65`

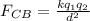
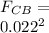
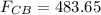
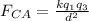
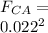
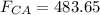
The net force acting on q1 is given by

`F_(3)=\sqrt{F_(CB)^(2)+F_(CA)^(2)+2F_(CB)F_(CA)Cos120}`

`F_(3)=\sqrt{483.65^(2)+483.65^(2)-2* 483.65* 483.65* 0.5}`

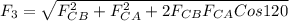
F3 = 483.65 N