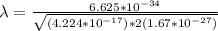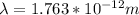Question

A proton is placed at point A, where the electric potential is 100 V . The proton is released from rest. Some time later, the proton has reached point B, where the electric potential is -120 V . What is the de Broglie wavelength of the proton when it reaches point B?

Answer 1

To develop this problem it is necessary to apply the concepts related to electromagnetic energy and Broglie's hypothesis.

By definition we know that the electrical energy of a proton can be expressed as

E = qV

Where,

q = Charge of proton

V = Voltage

Replacing with our values

E = qV

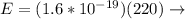`E = (1.6*10^(-19))(220) \rightarrow` It is necessary to add the two potentials

`E = 4.224*10^(-17)J`

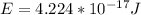
From Broglie's hypothesis we know that the wavelength is given by

`\lambda = (h)/(P)`

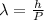
Where,

h = Planck's constant

p = Momentum

The momentum of a particle can be expressed in terms of energy, that is,

`P = √(E*2m)`

Where,

m = mass

E = Energy (potential or kinetic)

Therefore replacing this value at lambda,

`\lambda = (h)/(√(E*2m))`

`\lambda = \frac{6.625*10^(-34)}{\sqrt{(4.224*10^(-17))*2(1.67*10^(-27))}}`

`\lambda = 1.763*10^(-12)m`