Answer:
Number of teeth on pinion =
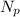 = 12
= 12
Explanation:
Given:
Gear ratio = 3 : 1 = 3
Diametral Pitch = P = 4
Center distance = c= 6 in
No. of teeth on Pinion =
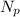 =?
=?
Gear ratio =
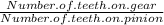 =
=
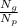 = 3
= 3
As Gear ratio = 3, so
Diameter ratio =
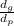 = 3
= 3
(Note : Diameter Ratio = Gear ratio )
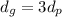 Equation 1
Equation 1
Center Distance = c =
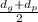 =
=
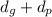 = 2 (c)
= 2 (c)
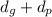 = 2 (6) = 12 in
= 2 (6) = 12 in
substitute
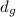 from equation 1, here
from equation 1, here
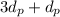 = 12
= 12
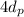 = 12
= 12
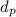 =
=
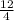 = 3
= 3
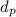 =3in
=3in
Now : Diametral Pitch =P=
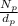
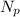 =
=
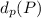
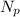 = 4 (3)
= 4 (3)
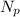 = 12
= 12
Which are the number of teeth on pinion