Question

Two uniform solid balls, one of radius R and mass M, the other of radius 2 R and mass 8 M, roll down a high incline. They start together from rest at the top of the incline. Which one will reach the bottom of the incline first?

Answer 1

First ball reaches at the bottom first.

Step-by-step explanation:

m1 = M

r1 = R

m2 = 8M

r2 = 2R

Moment of inertia of the solid ball is

I = 2/5 mr^2

So, the radius of gyration of the ball

`K=\sqrt{(2)/(5)}r`

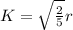
So,

`K_(1)=\sqrt{(2)/(5)}R`

`K_(2)=\sqrt{(2)/(5)}* 2R`

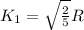
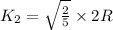
The ball having more acceleration reaches the first at the bottom of the inclined plane.

The acceleration is given by

`a=(gSin\theta )/(1+(K^(2))/(r^(2)))`

So,

`a_(1)=(gSin\theta )/(1+(2)/(5))=(5gSin\theta )/(7)`

`a_(2)=(gSin\theta )/(1+(8)/(5))=(5gSin\theta )/(13)`

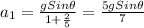
So, a1 > a2

Thus, the first ball reaches at the bottom first.