Question

The monthly worldwide average number of airplane crashes of commercial airlines is 2.2. What is the probability that there will be

(a) more than 2 such accidents in the next month?
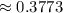
(b) more than 4 such accidents in the next 2 months?
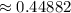
(c) more than 5 such accidents in the next 3 more than 5 such accidents in the next 3 months?

Answer 1

(a) more than 2 such accidents in the next month
`\approx 0.3773`

(b) more than 4 such accidents in the next 2 months
`\approx 0.44882`

(c) more than 5 such accidents in the next 3 more than 5 such accidents in the next 3 months
`\approx 0.64533`

Explanation:

Let N be the Random variable that marks the number of crashes in certain month.

Now let us use Poisson distribution since we are given with average number of crashes that is N \sim Pois(2.2)

(A) more than 2 such accidents in the next month

Probability(more than 2 such accidents in the next month)=P(N>2)

P(N>2)=1-P(N=0)-P(N=1)-P(N=2)

=>
`1-e^-{2.2}-2.2e^(-2.2)-(2.2^2)/(2!)e^(2.2)`

=>
`\approx 0.3773`

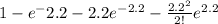
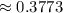
B) more than 4 such accidents in the next 2 months

since the average number of crashes in 1 month is 2.2, the average number of crashes in two months is 4.4. hence, if we say that
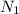`N_1` is the number of crashes in 2 months, we have that
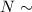`N\sim`Pois(4.4)

Thus,

Probability(more than 4 such accidents in the next 2 months)=P(
`N_1>4`)

=
`1-P(N_1=0)-P(N_1=1)-P(N_1=2)=P(N_1=3)-P(N_1=4)`

`1-\sum_(k=1)^(4) (4.4^(k))/(k !) e^(-4.4)`

=>
`\approx 0.44882`

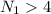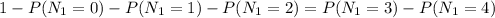
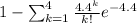
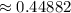
C) more than 5 such accidents in the next 3 more than 5 such accidents in the next 3 months

If we say that
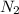`N_2` marks the number of crashes in the next 3 months , using the same argument as in (a) we have that a
`N\sim`Pois(6.6)

Hence

P(
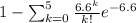
`N_2>5`)=
`1-\sum_(k=0)^(5) (6.6^(k))/(k !) e^(-6.6)`

=>
`\approx 0.64533`