Question

You drive from your home to a vacation resort 420 miles away. You return on the same highway. The average velocity on the return trip is 15 miles per hour slower than the average velocity on the outgoing trip. Express the total time required to complete the round​ trip, T, as a function of the average velocity on the outgoing​ trip, x.

Answer 1

Time required to complete the round​ trip
`T=(420)/(x)+(420)/((x-15))` where x is average velocity on the outgoing​ trip.

Explanation:

Let average velocity of outgoing trip = x mph

The average velocity on the return trip is 15 miles per hour slower than the average velocity on the outgoing trip.

Average velocity of return trip = (x-15) mph

Distance to vacation place = 420 miles

Distance to vacation place = Time for outgoing trip x average velocity of outgoing trip

`420=t_1* x\\\\t_1=(420)/(x)`

Distance to vacation place = Time for return trip x average velocity of return trip

`420=t_2* (x-15)\\\\t_2=(420)/((x-15))`

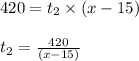
We have total time T = t₁ + t₂

That is

`T=(420)/(x)+(420)/((x-15))`

Time required to complete the round​ trip
`T=(420)/(x)+(420)/((x-15))` where x is average velocity on the outgoing​ trip.