To develop this problem it is necessary to apply the concepts related to destructive interaction.
By definition we know that it is given as

Where,
l = Distance between slits
m = Any integer representing the number of repetition of spectrum
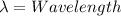
There is a change in phase at the upper side of the film which causes the phase shift since the index of refraction of the soap film is greater than that of air.
The extra traveled distance is twice the film thickness since the light shines perpendicularly and the wave travels back and fourth through the film, so
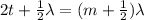

 (second smalles nonzero thickness) we have that
(second smalles nonzero thickness) we have that


The index of refraction of soap is given so the relationship is
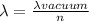
Substituting the previos equation
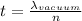
Re, arrange to find \lambda_{vacuum}

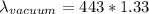
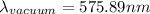
Therefore the vacuum wavelength of the light is 575.89nm