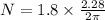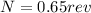Question

A diver comes off a board with arms straight up and legs straight down, giving her a moment of inertia about her rotation axis of 18 kg⋅m2. She then tucks into a small ball, decreasing this moment of inertia to 3.6 kg⋅m2. While tucked, she makes two complete revolutions in 1.1s. If she hadn't tucked at all, how many revolutions would she have made in the 1.8s from board to water?

Answer 1

N = 0.65 rev

Step-by-step explanation:

As we know that there is no external torque on the diver while she is in air

Now during her motion we can use angular momentum conservation as there is no torque on it

So we have

`I_1\omega_1 = I_2\omega_2`

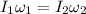
so we have

`18 * \omega_1 = 3.6 * \omega_2`

as we know that when she is in tucked position then

`\omega_2 = 2\pi (2)/(1.1)`

`\omega_2 = 11.4 rad/s`

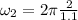
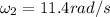
so we have

`18 * \omega_1 = 3.6 * 11.4`

`\omega_1 = 2.28 rad/s`

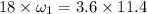
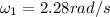
now we have number of revolutions in 1.8 s given as

`N = 1.8 * (2.28)/(2\pi)`

`N = 0.65 rev`