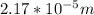Question

When subjected to a force of compression, the length of a bone (compression Young's modulus 9.4 x 109 N/m2, tensile Young's modulus 1.6 x 1010 N/m2) decreases by 3.7 x 10-5 m. When this same bone is subjected to a tensile force of the same magnitude, by how much does it stretch?

Answer 1

To solve this problem it is necessary to apply the definition of Young's Module which states that

`Y_1 = ((F)/(A))/((\Delta l_0)/(l))`

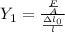
Where,

F = Force

A = Cross sectional Area

L = Length

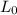`L_0` = Initial Length

We need to find the ratio between the two values when the another values are constant, that is

`(Y_1)/(Y_2) = (((F)/(A))/((\Delta l_1)/(l)))/(((F)/(A))/((\Delta l_2)/(l)))`

`(Y_1)/(Y_2) = (\Delta l_2)/(\Delta l_1)`

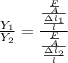
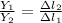
Re-arrange to find
`\Delta l_2,`

`\Delta l_2 = (9.4*10^9)/(1.6*10^(10))*3.7*10^(-5)`

`\Delta l_2 = 2.17*10^(-5) m`

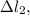
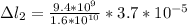
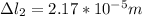
Therefore the bone stretch around
`2.17*10^(-5) m`