Question

A 1 036-kg satellite orbits the Earth at a constant altitude of 98-km. (a) How much energy must be added to the system to move the satellite into a circular orbit with altitude 198 km? MJ (b) What is the change in the system's kinetic energy? MJ (c) What is the change in the system's potential energy?

Answer 1

a) The Energy added should be 484.438 MJ

b) The Kinetic Energy change is -484.438 MJ

c) The Potential Energy change is 968.907 MJ

Step-by-step explanation:

Let 'm' be the mass of the satellite , 'M'(6×
`10^(24)` be the mass of earth , 'R'(6400 Km) be the radius of the earth , 'h' be the altitude of the satellite and 'G' (6.67×
`10^(-11)` N/m) be the universal constant of gravitation.

We know that the orbital velocity(v) for a satellite -

v=
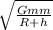`\sqrt{(Gmm)/(R+h) }` [(R+h) is the distance of the satellite from the center of the earth ]

Total Energy(E) = Kinetic Energy(KE) + Potential Energy(PE)

For initial conditions ,

h =
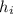`h_(i)` = 98 km = 98000 m

∴Initial Energy (
`E_(i)`) =
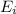`(1)/(2)`m
`v^(2)` +
`(-GMm)/((R+h_(i) ))`

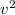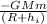
Substituting v=
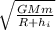`\sqrt{(GMm)/(R+h_(i) ) }` in the above equation and simplifying we get,

`E_(i)` =
`(-GMm)/(2(R+h_(i)) )`

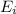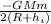
Similarly for final condition,

h=
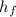`h_(f)` = 198km = 198000 m

∴Final Energy(
`E_(f)`) =
`(-GMm)/(2(R+h_(f)) )`

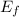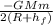
a) The energy that should be added should be the difference in the energy of initial and final states -

∴ ΔE =
`E_(f)` -
`E_(i)`

=
`(GMm)/(2)`(
`(1)/(R+h_(i) )` -
`(1)/(R+h_(f) )`)

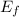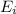
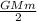Substituting ,

M = 6 ×
`10^(24)` kg

m = 1036 kg

G = 6.67 ×
`10^(-11)`

R = 6400000 m

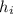`h_(i)` = 98000 m

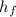`h_(f)` = 198000 m

We get ,

ΔE = 484.438 MJ

b) Change in Kinetic Energy (ΔKE) =
`(1)/(2)`m[
`v_(f) ^(2)` -
`v_(i) ^(2)`]

=
`(GMm)/(2)`[
`\frac{1} {R+h_(f) }` -
`\frac{1} {R+h_(i) }`]

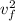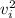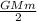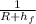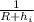= -ΔE

= - 484.438 MJ

c) Change in Potential Energy (ΔPE) = GMm[
`(1)/(R+h_(i) )` -
`(1)/(R+h_(f) )`]

= 2ΔE

= 968.907 MJ