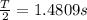Question

A 20.0-kg mass is traveling to the right with a speed of 2.40 m/s on a smooth horizontal surface when it collides with and sticks to a second 20.0-kg mass that is initially at rest but is attached to a light spring with force constant 180 N/m. (A) Find the amplitude of the subsequent oscillations. (B) Find the period of the subsequent oscillations. (C) How long does it take the system to return the first time to the position it had immediately after the collision?

Answer 1

a)
`A \approx 0.566\,m`, b)
`T \approx 2.962\,s`, c)
`\Delta t = 1.481\,s`

Step-by-step explanation:

a) The initial speed of the system formed by the two masses are determined by the Principle of Momentum Conservation:

`(20\,kg)\cdot (2.40\,(m)/(s) ) = (40\,kg)\cdot v`

`v = 1.20\,(m)/(s)`

The amplitude of the masses-spring system is determined with the help of the Principle of Energy Conservation, which states that:

`K = U_(k)`

`(1)/(2)\cdot (40\,kg)\cdot (1.20\,(m)/(s) )^(2) = (1)/(2)\cdot (180\,(N)/(m) )\cdot A^(2)`

The amplitude is:

`A \approx 0.566\,m`

b) The period of oscillation of the system is:

`T = 2\pi\cdot \sqrt{(40\,kg)/(180\,(N)/(m) ) }`

`T \approx 2.962\,s`

c) The time of return to the first position is equal to the half of the period of oscillation. That is to say:

`\Delta t = 0.5\cdot T`

`\Delta t = 1.481\,s`

Answer 2

To solve this problem it is necessary to apply the concepts related to the conservation of the moment, frequency, period and amplitude.

PART A) By definition we know that the conservation of the moment is expressed under the function

`m_1u_1+m_2u_2 = m_1v_1+m_2v_2`

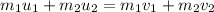
Where,

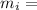`m_i =` Mass of each object

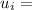`u_i =` Initial velocity of each object

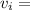`v_i =` Initial velocity of each object

Since the final velocity is the same for both objects, and body two does not have an initial velocity then,

`m_1u_1 = (m_1+m_2)v_2`

`20.0*2.4 = 40.0v_2`

`v_2=1.2 m/s`

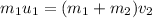
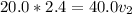
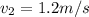
The kinetic energy transferred at the time of the collision is then given by

`E =(mv^2)/(2)`

`E =(1)/(2)(40)(1.2)^2`

`E =28.8J`

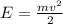
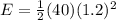
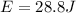
By laws of the conservation of Physics, the kinetic energy of the body is conserved and transformed into elastic potential energy, that is, the energy is transferred to the block until it reaches rest.

By definition this elastic potential energy can be expressed in terms of Amplitude, angular velocity and mass as (Simple harmonic motion):

`E = (1)/(2) m\omega^2 A^2`

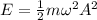
Where,

A = Amplitude

m = Total mass

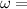`\omega =`Angular velocity, also expressed as,

`\omega = \sqrt{(k)/(M)}`

`\omega = \sqrt{(180)/(40)}`

`\omega = 2.1213rad/s`

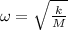
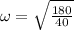
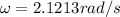
As there is energy conservation then,

`28.8J = (1)/(2) (40)(2.1213)^2 A^2`

`A = \sqrt{(2*28.8)/( (40)(2.1213)^2)}`

`A = 0.56569mm`

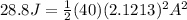
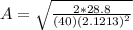
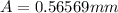
Therefore the Amplitude of the subsequent oscillation is 0.158m

PART B )

We calculate the value of the frequency for which we have to,

`f = (\omega)/(2\pi)`

`f = (2.060)/(2\pi)`

`f = 0.3376 Hz`

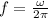
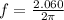
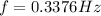
Therefore the period is

`T = (1)/(f)`

`T = (1)/(0.3376)`

`T =2.961s`

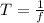
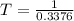
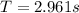
PART C) Finally we know that during the course of the body, this will go from a minimum initial position, to a maximum position and whose center of travel is its initial position.

The period of time used to go from the minimum to the maximum position is the total period. Therefore, if half of its route is its initial position, the time needed to return to this position will be half of the period. The time taken by the system to return to initial position for the first time:

`(T)/(2) = 1.4809s`