Question

The proper mean lifetime of a subnuclear particle called a muon is 2 µs. Muons in a beam are traveling at 0.902 c relative to a laboratory. The speed of light is 2.998 × 108 m/s. In the reference frame of the muon, how far does the laboratory travel in a typical lifetime of 2 µs?

Answer 1

To solve this problem it is necessary to apply the equations related to the time measured from a relative viewer and the mathematical equations of motion.

Speed is defined as

`v = (d)/(t)`

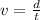
Where,

d = Distance

t = Time

Re-arrange to find d,

`d = vt \\d = 0.902c*(2*10^(-6))\\d = 0.902(2.998*10^8)*(2*10^(-6))\\d = 540.83m`

Applying the equations of relativity of time,

`t' = \frac{t_0}{\sqrt{1-(v^2)/(c^2)}}`

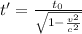
Where,

v = Velocity

c = speed of light

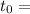`t_0 =` Reference time

t = relative time

Replacing,

`t' = \frac{2*10^(-6)}{\sqrt{1-((0.902c)^2)/(c^2)}}`

`t' = (2*10^(-6))/(1-0.902)}`

`t' = 2.04*10^(-5)s`

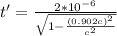
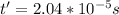
Therefore the distance would be

`d = vt'\\d = 0.902c*(2.04*10^(-5))\\d = 0.902(2.998*10^8)*(2.04*10^(-5))\\d = 5516.56m`

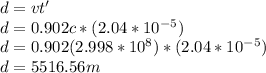
Therefore the travel will be 5.5Km