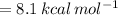Question

The gas-phase reaction follows an elementary rate law and is to be carried out first in a PFR and then in a separate experiment in a CSTR. When pure A is fed to a 10 dm 3 PFR at 300 K and a volumetric flow rate of 5 dm 3 /s, the conversion is 80%. When a mixture of 50% A and 50% inert (I) is fed to a 10 dm 3 CSTR at 320 K and a volumetric flow rate of 5 dm 3 /s, the conversion is also 80%. What is the activation energy in cal/mol

Answer 1

The activation energy is
`=8.1\,kcal\,mol^(-1)`

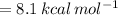
Step-by-step explanation:

The gas phase reaction is as follows.

`A \rightarrow B+C`

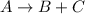
The rate law of the reaction is as follows.

`-r_(A)=kC_(A)`

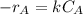
The reaction is carried out first in the plug flow reactor with feed as pure reactant.

From the given,

Volume "V" =
`10dm^(3)`

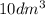
Temperature "T" = 300 K

Volumetric flow rate of the reaction
`v_(o)=5dm^(3)s`

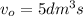
Conversion of the reaction "X" = 0.8

The rate constant of the reaction can be calculate by the following formua.

`V= (v_(0))/(k)[(1+\epsilon )ln((1)/(1-X)-\epsilon X)]`

Rearrange the formula is as follows.

`k= (v_(0))/(V)[(1+\epsilon )ln((1)/(1-X)-\epsilon X)]............(1)`

The feed has Pure A, mole fraction of A in feed
`y_{A_(o)}` is 1.

`\epsilon =y_{A_(o)}\delta`

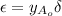
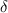`\delta` = change in total number of moles per mole of A reacte.

`=1(2-1)=1`

Substitute the all given values in equation (1)

`k=(5m^(3)/s)/(10dm^(3))[(1+1)ln (1)/(1-0.8)-1 * 0.8] = 1.2s^(-1)`

Therefore, the rate constant in case of the plug flow reacor at 300K is
`1.2s^(-1)`

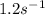
The rate constant in case of the CSTR can be calculated by using the formula.

`(V)/(v_(0))= (X(1+\epsilon X))/(k(1-X)).............(2)`

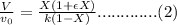
The feed has 50% A and 50% inerts.

Hence, the mole fraction of A in feed
`y_{A_(o)}` is 0.5

`\epsilon =y_{A_(o)}\delta`

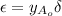
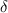`\delta` = change in total number of moles per mole of A reacted.

`=0.5(2-1)=0.5`

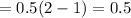
Substitute the all values in formula (2)

`(10dm^(3))/(5dm^(3))=(0.8(1+0.5(0.8)))/(k(1-0.8))=2.8s^(-1)`

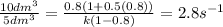
Therefore, the rate constant in case of CSTR comes out to be
`2.8s^(-1)`

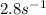
The activation energy of the reaction can be calculated by using formula

`k(T_(2))=k(T_(1))exp[(E)/(R)((1)/(T_(1))-(1)/(T_(2)))]`

In the above reaction rate constant at the two different temperatures.

Rearrange the above formula is as follows.

`E= R *((T_(1)T_(2))/(T_(1)-T_(2)))ln(k(T_(2)))/(k(T_(1)))`

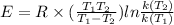
Substitute the all values.

`=1.987cal/molK((300K *320K)/(320K *300K))ln (2.8)/(1.2)=8.081 *10^(3)cal\,mol^(-1)`

`=8.1\,kcal\,mol^(-1)`

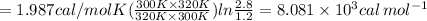
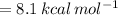
Therefore, the activation energy is
`=8.1\,kcal\,mol^(-1)`