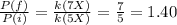Question

Ammonia and chlorine react to form nitrogen and hydrochloric acid. If you react 2.0 L of ammonia with 3.0 L of chlorine at constant temperature in a fixed volume container, what is the ratio of the final and initial pressures (Pria/Pinta? 2NH3(g) + 3Cl2 (g) → Nz (g) + 6HCI (8)

a. 0.71
b. 1.00
c. 1.40 d. 1.50
d. none of these

Answer 1

c) 1.40

Step-by-step explanation:

Ammonia and chlorine reacts according to the equation:

`2NH_(3)(g) + 3Cl_(2)(g)` →
`N_(2)(g) + 6HCl(g)`

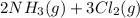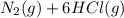
From the above balanced equation, we can infer that 2 mols of Ammonia reacts with 3 mols of Chlorine to form 1 mol of Nitrogen and 6 mols of Hydrogen-chloride gas. We also know that, the volume of a gas is directly proportional to the number of mols of the gas. Thus, if 2 mols of Nitrogen reacts with 3 mols of Chlorine completely, then 2 L of Ammonia will react with 3 L of Chlorine completely (We are provided with 2L of Ammonia and 3L of Chlorine). Thus, the reaction is a complete reaction. So, the number of mols of Ammonia initially is equal to 2X (where, X is some constant value), mols of Chlorine is equal to 3X. And for the final products, the number of mols of Nitrogen is equal to 1X and number of mols of Hydrogen chloride is equal to 6X.

Now, we know that pressure in a container is directly proportional to the number of mols of the gas in that container (i.e, P ∝ number of mols). Since the volume and temperature is constant for this particular reaction, the pressure change in the process is due to the change in number of mols of the reactants and products.

Here, initial pressure, P(i) ∝ initial number of mols, i.e, P(i) = k(2X + 3X) (where k is a constant)

final pressure, P(f) ∝ final number of mols, i.e, P(f) = k(1X + 6X)

Hence, the ratio between final and initial pressure is:
`(P(f))/(P(i)) = (k(7X))/(k(5X)) = (7)/(5) = 1.40`