Question

How many different four-digit even positive integers can be made using the digits 1, 2, 3, 4, 5 if no digit can be used more than once?

Answer 1

120 different four-digit even positive integers can be made using the digits 1, 2, 3, 4, 5 if no digit can be used more than once

Solution:

Given, digits are 1, 2, 3, 4, 5

We have to find the number of ways in which 4 digit number can be made form the given digits with out repetition.

Now, first we have to select 4 digits out of 5 digits to form a number.

As it is just combination, we can take in
`^(5) \mathrm{C}_(4) \text { Ways. }`

`\mathrm{n} \mathrm{C}_{\mathrm{r}}=(n !)/((n-r) ! r !)`

`5 \mathrm{C}_(4)=(5 !)/((5-4) ! 4 !)=(5 * 4 !)/(1 ! 4 !)=5`

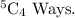
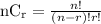
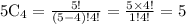
So, we can select 4 digits in 5 ways.

And now, we can arrange them in 4! Factorial ways.

Then, total 5 x 4! Ways are available

`5 * 4 !=5 !=5 * 4 * 3 * 2 * 1=120 \text { ways }`

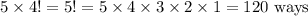
Hence, we can form 120 different numbers.