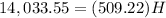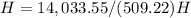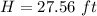Question

the base of a regular pyramid is a hexagon whose perimeter is 84 feet. the volume of the pyramid is approximately 4,677.85 cubic feet. find the height of the pyramid.

Answer 1

The height of the pyramid is
`27.56\ ft`

Explanation:

we know that

The volume of the pyramid is equal to

`V=(1)/(3)BH`

where

B is the area of the base of the pyramid

H is the height of the pyramid

step 1

Find the area B of the regular hexagonal base

we know that

The perimeter of a regular hexagon is

`P=6b`

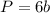
where

b is the length side of the hexagon

we have

`P=84\ ft`

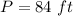
substitute

`84=6b`

solve for b

`b=14\ ft`

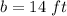
Remember that the area of a regular hexagon is the same that the area of six equilateral triangles

Determine the area of the six equilateral triangles, applying the formula of the law of sines

`B=6[(1)/(2)b^2sin(60\°)]`

substitute the value of b

`B=6[(1)/(2)(14)^2sin(60\°)]`

`B=509.22\ ft^2`

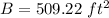
step 2

Find the height of the pyramid

`V=(1)/(3)BH`

we have

`V=4,677.85\ ft^3`

`B=509.22\ ft^2`

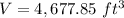
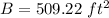
substitute

`4,677.85=(1)/(3)(509.22)H`

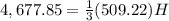
solve for H

`14,033.55=(509.22)H`

`H=14,033.55/(509.22)H`

`H=27.56\ ft`