Answer:
The equation of line Le is 5 y + x + 89 = 0
Explanation:
Given as :
The line Li passes through point (1,2)
The slope of line Li (m) = 5
So, equation of line y = m x + c
or, 2 = 5 × 1 + c
Or, c = 2 - 5 = -3
∴ Eq of line Li is
y = 5 x - 3
Another line Le is perpendicular to line Li
Let the slope of line Le = M
The line Le meet at points where x = 4
So, for perpendicular property
Products of slopes = - 1
So, m × M = - 1
or, M = -

Or. M = -
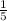
Now equation of line Le is y = M x + c
∵ Line Le meet the line Li at x = 4
So, y = 5 × 4 - 3
I.e y = 20 - 3
Or, y = 17
Now, equation of line Le with slope -
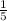 and passes through points ( 4 , 17 ) is
and passes through points ( 4 , 17 ) is
y = M x + c
or, 17 = -
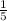 × 4 + c
× 4 + c
or, 17 +
 = c
= c
So, c =
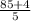
Or, c = -

∴ Equation of line Le is y = -
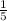 x -
x -

ie. 5 y = - x - 89
or, 5 y + x + 89 = 0
Hence The equation of line Le is 5 y + x + 89 = 0 answer