Answer:
131
Explanation:
Note that the difference between consecutive terms is constant, that is
8 - 5 = 11 - 8 = 14 - 11 = 17 - 14 = 3
This indicates that the terms form an arithmetic sequence with
 = a₁ + (n - 1)d
= a₁ + (n - 1)d
where a₁ is the first term and d the common difference
Here a₁ = 5 and d = 3, thus
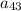 = 5 + (42 × 3) = 5 + 126 = 131
= 5 + (42 × 3) = 5 + 126 = 131