Answer:
Isosceles triangle
Explanation:
It is assumed that the triangle is a right angle triangle, implying that Pythagoras theorem becomes applicable.
If the first side is represented by x and the second side by y,
x + y = 5
The hypotenuse is always the longest side hence it can be presumed to be 4 since both x and y cannot be more than 5.
Therefore using pythagoras equation:
hyp^2 = sqrt(opp^2 + adj^2)
this implies that
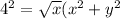
therefore
16 = sqrt (x^2 + y^2) ----------------- (i)
since x + y = 5, y = 5 - x ------------------- (ii)
substituting (ii) into eqn (i)
16 = sqrt ( x^2 + (5-X)^2)
16 = sqrt( x^2 + 25 -10x + x^2)
16 = sqrt( x^2 + x^2 - 10x + 25)
16 = sqrt( 2x^2 - 10x + 25)
squaring both sides
256 = 2x^2 - 10x + 25
this can be refined as
2x^2 - 10x - 231 = 0
Solving using quadratic equation:
where a = 2, b = -10 and c = -231
x = 13.53 or -8.53.
Since x is a side of a triangle that cannot be negative,
x = 13.53 but x can never be greater than 5 since x + y = 5
This implies that the triangle is not a right angle triangle; it is most likely an isosceles triangle with two sides of equal length such that x = y = 2.5 inches while the longest side; the hypotenuse is 4 inches.
substituting for x in