Question

Find the maximum number of lines per centimeter a diffraction grating can have and produce a first-order maximum for the largest wavelength of visible light. (Assume the wavelengths of visible light range from 380 nm to 760 nm in a vacuum.)

Answer 1

To solve this problem it is necessary to apply the concepts related to constructive interference for multiple split.

The precaution is given by,

`dsin\theta = m\lambda`

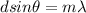
Where,

d = Distance between the slits

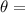`\theta =` Angle between the path and a line from the slits to the screen

m = Any integer, representing the number of repetition of the spectrum.

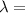`\lambda =`Wavelength

For first order equation we have that m = 1 then

`d sin\theta = \lambda`

As the maximum number of lines corresponds to the smallest d values, we have that
`\theta = 90`

`d sin90=\lambda`

`d = 760nm`

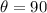
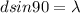
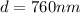
Therefore the maximum numbers of lines per centimeter would be

`N = (10^(-2)m)/(d)`

`N = (10^(-2)m)/(760*10^(-9)m)`

`N = 13157.89`

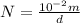
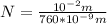
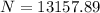
The maximum numbers of lines per centimeter is 13158