Question

A 94.0 N grocery cart is pushed 17.6 m along an aisle by a shopper who exerts a constant horizontal force of 42.6 N. The acceleration of gravity is 9.81 m/s 2 . If all frictional forces are neglected and the cart starts from rest, what is the grocery cart’s final speed

Answer 1

vf = 12.51 m/s

Step-by-step explanation:

Newton's second law to the grocery cart:

∑F = m*a Formula (1)

∑F : algebraic sum of the forces in Newton (N)

m : mass s (kg)

a : acceleration (m/s²)

We define the x-axis in the direction parallel to the movement of the grocery cart and the y-axis in the direction perpendicular to it.

Forces acting on the grocery cart

W: Weight of the block : In vertical direction downward

N : Normal force : In vertical direction upward

F : horizontal force

Calculated of the mas of the grocery cart (m)

W = m*g

m = W/g

W = 94.0 N , g = 9.81 m/s²

m = 94/9.81

m = 9.58 Kg

Calculated of the acceleration of the grocery cart (a)

∑F = m*a

F = m*a

42.6 = (9.58)*a

a = (42.6) / (9.58)

a = 4.45 m/s²

Kinematics Equation of the grocery cart

Because the grocery cart moves with uniformly accelerated movement we apply the following formula to calculate its final speed :

vf²=v₀²+2*a*d Formula (2)

Where:

d:displacement (m)

v₀: initial speed (m/s)

vf: final speed (m/s)

a: acceleration (m/s²)

Data:

v₀ = 0

a = 4.45 m/s²

d = 17.6 m

We replace data in the formula (2) :

vf²=v₀²+2*a*d

vf² = 0+2*(4.45)*(17.6)

vf² = 156.64

`v_(f) = √(156.64)`

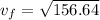
vf = 12.51 m/s