Question

(a) How long will it take an 850-kg car with a useful power output of 40.0 hp (1 hp equals 746 W) to reach a speed of 15.0 m/s, neglecting friction? (b) How long will this acceleration take if the car also climbs a 3.00-m high hill in the process?

Answer 1

(A) time = 3.205 s

(B)time =4.04 s

Step-by-step explanation:

mass (m) = 850 kg

power (P) = 40 hp = 40 x 746 = 29,840 W

final velocity (Vf) = 15 m/s

final height (Hf) = 3 m

since the car is starting from rest at the bottom of the hill, its initial velocity and initial height are both 0

(A) from the work energy theorem

• work = 0.5 x m x (
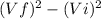  `(Vf)^(2) - (Vi)^(2)`) (change in kinetic energy)
• work = power x time
• therefore

power x time = 0.5 x m x (
`(Vf)^(2) - (Vi)^(2)`)

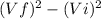time =
)}{power}[/tex]

time =
)}{29,840}[/tex]

time = 3.205 s

(B) from the work energy theorem

• work = change in potential energy + change in kinetic energy

• work = (mg (Hf - Hi)) + (0.5m(
  `(Vf)^(2) - (Vi)^(2)`)

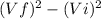• work = power x time
• therefore

power x time = (mg (Hf - Hi)) + (0.5m(
`(Vf)^(2) - (Vi)^(2)`)

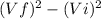time =
)}[/tex])}{power}[/tex]

time =
)}[/tex])}{29,840}[/tex]

time =4.04 s

Answer 2

a)
`\Delta t = 3.205\,s`, b)
`\Delta t = 4.043\,s`

Step-by-step explanation:

a) The time needed is determined by the Work-Energy Theorem and the Principle of Energy Conservation:

`K_(1) + \Delta E = K_(2)`

`\Delta E = K_(2) - K_(1)`

`\dot W \cdot \Delta t = (1)/(2)\cdot m \cdot v^(2)`

`\Delta t = (m\cdot v^(2))/(2\cdot \dot W)`

`\Delta t = ((850\,kg)\cdot \left(15\,(m)/(s) \right)^(2))/(2\cdot (40\,hp)\cdot \left((746\,W)/(1\,hp) \right))`

`\Delta t = 3.205\,s`

b) The time is found by using the same approach of the previous point:

`U_(1) + K_(1) + \Delta E = U_(2) + K_(2)`

`\Delta E = (U_(2)-U_(1))+(K_(2) - K_(1))`

`\dot W \cdot \Delta t = m\cdot \left(g\cdot \Delta h + (1)/(2)\cdot v^(2) \right)`

`\Delta t = (m\cdot\left(g\cdot \Delta h + (1)/(2)\cdot v^(2)\right))/(\dot W)`

`\Delta t = ((850\,kg)\cdot \left[\left(9.807\,(m)/(s^(2)) \right)\cdot (3\,m) + (1)/(2)\cdot \left(15\,(m)/(s) \right)^(2)\right])/((40\,hp)\cdot \left((746\,W)/(1\,hp) \right))`

`\Delta t = 4.043\,s`