Question

. The joint density function of X and Y is given by f ( x , y ) = x e − x ( y + 1 ) x > 0 , y > 0 Find the conditional density of X , given Y = y , and that of Y , given X = x . Find the density function of Z = X Y .

Answer 1

The marginal probability density functions of X and Y are
`x^2` and
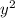`y^2`, respectively. X and Y are not independent. The conditional probability density functions of X given Y = y and Y given X = x are 2x and 2y, respectively. The density function of Z =
`X^2 + Y^2 is 2z / π(1 + z^2)`.

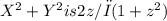Marginal probability density function of X: f_X(x) = ∫₀¹ 2xy dy =
`x^2`, 0 < x < 1

Marginal probability density function of Y:

f_Y(y) = ∫₀¹ 2xy dx =
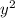`y^2`, 0 < y < 1

Independence of X and Y:

Since the joint probability density function f(x, y) is not a product of the marginal probability density functions f_X(x) and f_Y(y), X and Y are not independent.

Conditional probability density function of X given Y = y:

f_X|Y(x|y) = (2xy) /
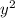`y^2` = 2x, 0 < x < 1

Conditional probability density function of Y given X = x:

f_Y|X(y|x) = (2xy) /
`x^2` = 2y, 0 < y < 1

Density function of Z =
`X^2 + Y^2`:

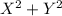To obtain the density function of Z, we need to perform the transformation of variables from (X, Y) to (Z, θ), where θ =
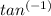`tan^{(-1)`(Y/X).

The joint density function of Z and θ is given by:

g(z, θ) = 2z /
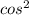`cos^2`(θ), 0 < z < ∞, 0 < θ < π/2

The density function of Z can be obtained by integrating g(z, θ) over all possible values of θ for a given value of z:

f_Z(z) = 2z / π(1 +
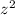`z^2`), 0 < z < ∞

Complete question:

The joint probability density function of random variables X and Y is given by:

f(x, y) = 2xy, 0 < x < 1, 0 < y < 1

Find the marginal probability density functions of X and Y.

Determine if X and Y are independent.

Find the conditional probability density function of X given Y = y.

Find the conditional probability density function of Y given X = x.

Find the density function of the random variable Z =
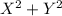`X^2 + Y^2`.

Answer 2

View answers attached as pictures below.