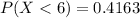A certain tennis player makes a successful first serve 64% of the time. Assume that each serve is independent of the others. If she serves 9 times, what's the probability…

Question

asked Sep 8, 2020 229k views

1 Answer

Erdikanik · Answer 1 · 2020-09-14T14:35:10+0000

Answer:

0.0181,0.2693,0.1092,0.4163

Explanation:

Given that a certain tennis player makes a successful first serve 64% of the time.

Since each serve is independent of the other

X the no of serves in is Binomial with n = no of times he serves =9

and p = constant probability = 0.64

X is Bin (9,0.64)

Probability that she get in

a) all 9 serves in?

=
$P(X=9) = 0.64^9\\=0.0181$

b) exactly 6 serves in?

P(x=6)

=
$9C6 (0.64)^6 (1-0.64)^3\\=0.2693$

c) at least 7 serves in

=
$P(X\geq 7) = 0.1092$

d) no more than 6 serves in

=
P(X<6)= 0.4163