Question

A long pipe of outer radius ????1=3.50 cm and inner radius ????2=2.98 cm carries a uniform charge density of 9.22 mC/m3. Assuming that the pipe is sufficiently long to consider it infinitely long, use Gauss's law to calculate the electric field ???? at a distance ????=7.35 cm from the centerline of the pipe. Use ????0=8.85×10−12 C/N·m2 for the the permittivity of free space.

Answer 1

2388078.86544 N/C

Step-by-step explanation:

`\rho` = Charge density = 9.22 mC/m³

r = Distance = 7.35 cm

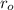`r_o` = Outer radius = 3.5 cm

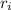`r_i` = Inner radius = 2.98 cm

l = Length of cylinder

`\epsilon_0` = Permittivity of free space =
`8.85* 10^(-12)\ F/m`

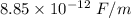
V = Volume

E = Electric field

Charge is given by

`Q=\rho V\\\Rightarrow Q=\rho\pi l(r_o^2-r_i^2)`

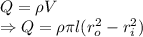
Area

`A=2\pi rl`

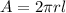
From Gauss law the flux through a cylindrical surface is given by

`EA=(Q)/(\epsilon_0)\\\Rightarrow E=(Q)/(\epsilon_0A)\\\Rightarrow E=(\rho\pi l(r_o^2-r_i^2))/(\epsilon_02\pi rl)\\\Rightarrow E=(\rho(r_o^2-r_i^2))/(\epsilon_02r)\\\Rightarrow E=(9.22* 10^(-3)(0.035^2-0.0298^2))/(8.85* 10^(-12)* 2* 0.0735)\\\Rightarrow E=2388078.86544\ N/C`

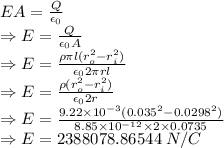
The electric at the given distance is 2388078.86544 N/C