Question

A manufacturer of interocular lenses will qualify a new grinding machine if there is evidence that the percentage of polished lenses that contain surface defects does not exceed 2%. A random sample of 250 lenses contains 6 defective lenses.

(a) Formulate and test an appropriate set of hypotheses to determine whether the machine can be qualified. Use α = 0.05. Find the P-value.
(b) Explain how the question in part (a) could be answered with a confidence interval. 9-97. A researcher claims th

Answer 1

Does not exceed 2% in both cases.

Explanation:

Given that a manufacturer of interocular lenses will qualify a new grinding machine if there is evidence that the percentage of polished lenses that contain surface defects does not exceed 2%.

Sample proportion =
`(6)/(250) \\=0.024`

Create hypothesses as

`H_0: p = 0.02\\H_a : p >0.02`

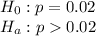
(Right tailed test at 5% significance level)

P difference = 0.004

Std error = 0.0089

test statistic Z = p diff/std error = 0.4518

p value = 0.326

Since p >alpha, we accept nullhypothesis

b) For confidence interval 97% we have

Margin of error = 2.17* std error = 0.0192

Confidence interval

=
`(0.024-0.0191, 0.024+0.0191)\\= (0.0049, 0.0431)\\`

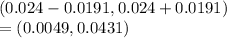
Since 2% = 0.02 lies within this interval we accept null hypothesis.

Does not exceed 2%

Since