Answer:
f = 63.8 N
Step-by-step explanation:
initial angle to the vertical = 5 degrees
initial holding force = 40 N
final angle to the vertical = 8 degrees
final holding force = ?
find the final holding force
m = mass and g = acceleration due to gravity
- for the initial holding force:
40 = mgSin5
mg =
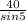 ....equation 1
....equation 1
- for the final holding force:
f = mgSin8 ......equation 2
substituting the value of mg from equation 1 (where mg =
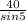 ) into equation 2
) into equation 2
f = mgSin8 =
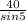 x Sin8
x Sin8
f = 63.8 N