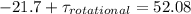Answer
given,
rotation of disk is equal to(θ) = 25.9
time taken = 5 s
moment of inertia of disk = 4 Kg.m²
disk come to rest in = 12 sec
a) θ = 2 π x 25.9
θ = 162.73 rad
using equation of rotational motion
θ = ω₀t + 0.5 α t²
162.79 = 0 + 0.5 x α x 5²
α = 13.02 rad/s²
total torque acting
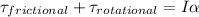
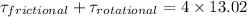
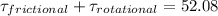
again using the rotational equation

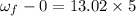
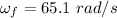
when only friction is acting angular acceleration

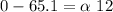
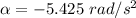
now torque due to friction
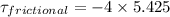
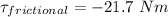
now,