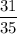Question

Consider a collection of envelopes consisting of 3 red envelopes​, 3 blue envelopes​, 1 green envelope​, and 3 yellow envelopes. If three envelopes are selected at​ random, without​ replacement, determine the probability that at least one envelope is a red envelope. The probability that at least one envelope is red is

Answer 1

Answer: Our required probability is
`(31)/(35)`

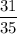
Explanation:

Since we have given that

Number of red envelopes = 3

Number of blue envelopes = 3

Number of green envelopes = 1

We need to select 3 envelopes in such a way that at least one envelope is a red.

So, it becomes,

`(^3C_1* ^4C_2)/(^7C_3)+(^3C_2* ^4C_1)/(^7C_3)+(^3C_3)/(7C_3)\\\\=(18)/(35)+(12)/(35)+(1)/(35)\\\\=(18+12+1)/(35)\\\\=(31)/(35)`

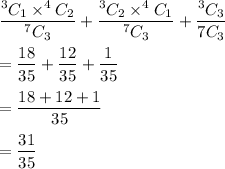
Hence, our required probability is
`(31)/(35)`