Question

2 Construct a rational function that will help solve the problem. Then, use a calculator to answer the question.

An open box with a square base is to have a volume of 500 cubic inches. Find the dimensions of the box that will have

minimum surface area. Let x = length of the side of the base.

Show your work:

Answer 1

Dimension of box:-

Side of square base = 10 in

Height of box = 5 in

Minimum Surface area, S = 300 in²

Explanation:

An open box with a square base is to have a volume of 500 cubic inches.

Let side of the base be x and height of the box is y

Volume of box = area of base × height

`500=x^2y`

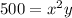
Therefore,
`y=(500)/(x^2)`

It is open box. The surface area of box, S .

`S=x^2+4xy`

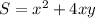
Put
`y=(500)/(x^2)`

`S(x)=x^2+(2000)/(x)`

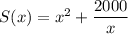
This would be rational function of surface area.

For maximum/minimum to differentiate S(x)

`S'(x)=2x-(2000)/(x^2)`

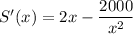
For critical point, S'(x)=0

`2x-(2000)/(x^2)=0`

`x^3=1000`

`x=10`

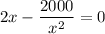
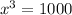
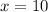
Put x = 10 into
`y=(500)/(x^2)`

y = 5

Double derivative of S(x)

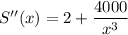`S''(x)=2+(4000)/(x^3)` at x = 10

`S''(10) > 0`

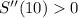
Therefore, Surface is minimum at x = 10 inches

Minimum Surface area, S = 300 in²