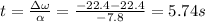Answer:
5.74s
Step-by-step explanation:
We can first solve for the initial angular velocity using the following formula
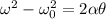
Where
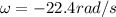 is the final angular velocity,
is the final angular velocity,
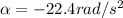 is the angular acceleration and
is the angular acceleration and
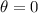 is the angular displacement
is the angular displacement

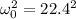
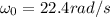
So for the wheel to get from 22.4 to -22.4 with angular acceleration of -7.8 then the time it takes must be