Question

The following data were collected from 12 rain gauges in a park. Build a 95% CI for the mean rainfall at the park.

4.65 3.89 2.73 4.35 3.80 4.86 4.33 4.37 4.76 4.05 3.05 3.87

1. Copy the data and paste into Excel. If you use Paste>Paste Special>Text, it should appear in a column.
2. Compute the sample mean and sample standard deviation. Use the function wizard or type =AVERAGE(Data range) and =STDEV.S(Data Range)
3. Find the critical value t* Use the formula for a CI to find upper and lower endpoints

Answer 1

Critical values:
`t_(\alpha/2)=-2.201`
`t_(1-\alpha/2)=2.201`

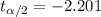
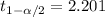
95% confidence interval would be given by (3.646;4.472)

Explanation:

1) Previous concepts

A confidence interval is "a range of values that’s likely to include a population value with a certain degree of confidence. It is often expressed a % whereby a population means lies between an upper and lower interval".

The margin of error is the range of values below and above the sample statistic in a confidence interval.

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

The data is:

4.65 3.89 2.73 4.35 3.80 4.86 4.33 4.37 4.76 4.05 3.05 3.87

2) Compute the sample mean and sample standard deviation.

In order to calculate the mean and the sample deviation we need to have on mind the following formulas:

`\bar X= \sum_(i=1)^n (x_i)/(n)`

`s=\sqrt{(\sum_(i=1)^n (x_i-\bar X))/(n-1)}`

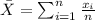
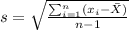
=AVERAGE(4.65,3.89,2.73, 4.35, 3.8, 4.86, 4.33, 4.37, 4.76, 4.05, 3.05, 3.87)

On this case the average is
`\bar X= 4.059`

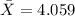
=STDEV.S(4.65,3.89,2.73, 4.35, 3.8, 4.86, 4.33, 4.37, 4.76, 4.05, 3.05, 3.87)

The sample standard deviation obtained was s=0.6503

3) Find the critical value t* Use the formula for a CI to find upper and lower endpoints

In order to find the critical value we need to take in count that our sample size n =12 <30 and on this case we don't know about the population standard deviation, so on this case we need to use the t distribution. Since our interval is at 95% of confidence, our significance level would be given by
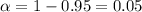`\alpha=1-0.95=0.05` and
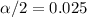`\alpha/2 =0.025`. The degrees of freedom are given by:

`df=n-1=12-1=11`

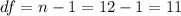
We can find the critical values in excel using the following formulas:

"=T.INV(0.025,11)" for
`t_(\alpha/2)=-2.201`

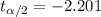
"=T.INV(1-0.025,11)" for
`t_(1-\alpha/2)=2.201`

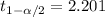
The confidence interval for the mean is given by the following formula:

`\bar X \pm t_(\alpha/2)(s)/(√(n))`

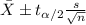
And we can use Excel to calculate the limits for the interval

Lower interval : "=4.059 -2.201*(0.6503/SQRT(12))" =3.646

Upper interval : "=4.059 +2.201*(0.6503/SQRT(12))" =4.472

So the 95% confidence interval would be given by (3.646;4.472)