Answer:
We can be 95% confident that the true proportion of citizens opposing a handgun ban is within 1.6% of the sample result.
is true.
Explanation:
Given that a television news program conducts a call in poll about a proposed city ban on handgun ownership. Of the 2372 calls,1921 oppose the ban. The station, following recommended practice, makes a confidence statement:
Sample proportion p =
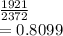
q=1-p =
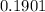
Std error of p =
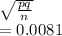
Margin of error for 95%=1.96*std error = 0.0158
Since margin of error is 0.0158 i.e. nearly 15.8% and proportion is 0.8099 = 81%
the statement is correct.
We can be 95% confident that the true proportion of citizens opposing a handgun ban is within 1.6% of the sample result.
is true.