Answer:
Q- 8 ) The value of x is 48 feet
Q-9 ) The value of x is 10
Explanation:
Given two figures as :
8 ) Let AB = 3 ft
AO = 5 ft
PQ = x ft
PO = 80 ft
Now, From figure ,
AB║PQ
∠ AOB = ∠ POQ ( vertically opposite angles )
∠ A = ∠ P
So , Δ AOB
 Δ POQ
Δ POQ
Now From similar triangle property
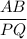 =
=
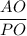
Or,
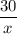 =
=
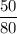
Or, x =
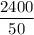
∴ x = 48 feet
9 ) Now, From the figure
ABC is a large Triangle and ADE is a small triangle
So, To prove both are similar
Since DE ║ BC
∠ ADE = ∠ ABC corresponding angles
and , ∠ AED = ∠ ACB corresponding angles
So, by angle angle
Δ ADE
 Δ ABC
Δ ABC
Now, From the similarity property
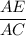 =
=

Or,
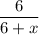 =
=
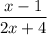
Or, 6 × ( 2 x + 4 ) = ( x - 1 ) × (6 + x )
Or, 12 x + 24 = 6 x + x² - 6 - x
Or, 12 x - 5 x + 30 = x²
or, x² - 7 x - 30 = 0
Or, x² - 10 x + 3 x - 30 = 0
or, x ( x - 10 ) + 3 ( x - 10 ) = 0
Or , ( x - 10 ) ( x + 3 ) = 0
∴ x = 10 , - 3
so, positive value of x is consider , i.e x = 10
Hence The value of x for Q- 8 is 48 feet
And the value of x for Q-9 is 10 . Answer