Answer:
71.4583 Hz
67.9064 N
Step-by-step explanation:
L = Length of tube = 1.2 m
l = Length of wire = 0.35 m
m = Mass of wire = 9.5 g
v = Speed of sound in air = 343 m/s
The fundamental frequency of the tube (closed at one end) is given by
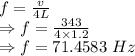
The fundamental frequency of the wire and tube is equal so he fundamental frequency of the wire is 71.4583 Hz
The linear density of the wire is
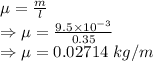
The fundamental frequency of the wire is given by
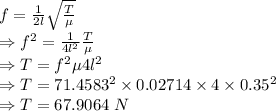
The tension in the wire is 67.9064 N