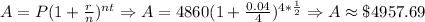Question

9. Alicia Martin's savings account has a principle of $1,200. It earns 6% interest compounded quartly

for two quarters

10. Aubrey Daniel's savings account has a principle of $5,725. It earns 4% interest compounded

quarterly for 3 years.

11. The principle of Angelo Carrera's savings account is $9,855. It earns 6% interest compounded

quarterly for 2 quarters.

12. Milo Simpson deposited $860 in a new regular savings account that's earns 5.5% interest

compounded semiannually for 1 year,

13. Jana Lacey deposits $4,860in a new credit union savings account on the first day of the quarter.

The principle earns 4% interest compounded quarterly for 6 months.

Answer 1

`9) \$1236.27\,10)\,\$6451.07\, 11)\,\$10,152.87 \,12)\,\$907.95 \,13)\,\$4957.69`

Explanation:

9) Since Alicia Martin's savings earns 6% quarterly for two quarters then:

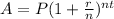`A=P(1+(r)/(n))^(nt)` ⇒ Amount (A), Principle (P), rate (r) in decimal form, number of compoundings (n) a year and t, in year or its fractions.

`A=P(1+(r)/(n))^(nt)\Rightarrow A=1200(1+(0.06)/(4))^{4*(1)/(2)}\Rightarrow A=\$1236.27`

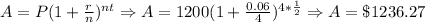
10) Aubrey Daniel's case:

`A=P(1+(r)/(n))^(nt)\Rightarrow A=5725(1+(0.04)/(4))^(4*3)\Rightarrow A\approx \$6451.07`

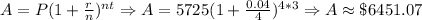
11) As for Angelo, similarly to Alicia.

`A=P(1+(r)/(n))^(nt)\Rightarrow A=9855(1+(0.06)/(4))^{4*(1)/(2)}\Rightarrow A\approx \$10,152.87`

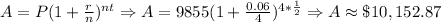
12) Simpson's. For semiannual n=2

`A=P(1+(r)/(n))^(nt)\Rightarrow A=860(1+(0.055)/(2))^(2*1)\Rightarrow A\approx \$907.95`

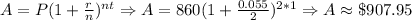
13) Jana Lacey amount:

`A=P(1+(r)/(n))^(nt)\Rightarrow A=4860(1+(0.04)/(4))^{4*(1)/(2)}\Rightarrow A\approx \$4957.69`