Question

Help fill out the proof

Answer 1

Step V: Transitive property of Inequality

Step VI: Subtraction Property of Inequality

Explanation:

In Step IV, the RHS of t=both the sides are equal.

So, they equated the LHS of both the sides.

This is the transitive property of equality which states that if a = b and c = b then a = c.

In this case, a =
`$ \angle {m_1} + \angle {m_2}  $`

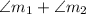
b = 180⁰

c =
`$ \angle {m_2} + \angle {m_3} $`

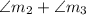
Consequently,
`$ \angle {m_1} + \angle {m_2} = \angle {m_2} + \angle {m_3} $`

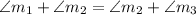
In step VI,
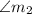`$ \angle {m_2} $` is subtracted on both the sides. So, this is called as Subtraction Property of Equality.