Question

The two pucks of equal mass did not move linearly (they came to a stop) after the collision due to the conservation of linear momentum. However, since the two pucks, mutual center of mass does not coincide with either of the pucks velocity vectors, they have angular momentum. This becomes evident after the collision when due to conservation of angular momentum the two pucks spin around their mutual center of mass.

Suppose we replace both hover pucks with pucks that are the same size as the originals but twice as massive. Otherwise, we keep the experiment the same. Compared to the pucks above, this pair of pucks will rotate:

a. at the same rate.
b. one-fourth as fast.
c. four times as fast.
d. twice as fast.
e. one-half as fast.

Answer 1

Compared to the pucks given, the pair of pucks will rotate at the same rate.

Answer: Option A

Step-by-step explanation:

The law of conservation of the angular momentum expresses that when no outer torque follows upon an article, no difference in angular momentum will happen. At the point when an item is turning in a shut framework and no outside torques are applied to it, it will have no change in angular momentum.

The conservation of the angular momentum clarifies the angular quickening of an ice skater as she brings her arms and legs near the vertical rotate of revolution. In the event, that the net torque is zero, at that point angular momentum is steady or saved.

By twice the mass yet keeping the speeds unaltered, also twice the angular momentum's to the two-puck framework. Be that as it may, we likewise double the moment of inertia. Since
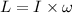`L=I * \omega`, the turning rate of the two-puck framework must stay unaltered.